Views
Book section 13.1
Definition: A view (i.e., projection) shows a defined subset of a model’s details, possibly with a transformation.
13.1 Projection (view) relationship
Cartographers have invented many projections of the Earth’s curved surface onto a flat map. Each requires a mathematical function that maps (i.e., projects) a spherical surface onto a planar surface. Perhaps the best known is the Mercator projection, invented in 1569, which has the property that all lines of longitude and latitude intersect at right angles. On the Earth’s surface, such intersections occur only at the equator, so as a consequence the Mercator projection exaggerates the size of land that is far from the equator. While falsely depicting Greenland as larger than Africa, this projection had the beneficial property that sailors wanting to get from one place to another can draw a line between the two and simply sail at that compass bearing. The Gall-Peters projection seeks to represent accurate sizes of countries but sacrifices the property of simple navigation.
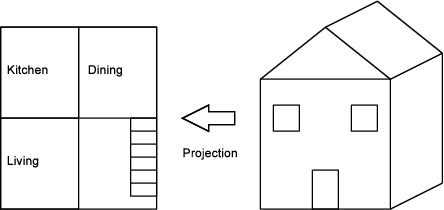
A projection, which you can use interchangeably with the term view, can be informally thought of as what something looks like from a particular perspective. More formally, a projection shows a defined subset of a model’s details, possibly transformed. A projection can remove details, such as a map that omits country boundaries. It can also transform the model, as seen in how the Mercator and Gall-Peters projections choose their transformations for easy navigation or accurate area. However, a projection cannot add information that does not already exist — it would be quite surprising to project the globe onto a piece of paper and discover a new continent. Projections are used when creating blueprints of houses. While a three-dimensional house is being designed, two-dimensional drawings of the house are produced. Each of these 2-D drawings is a projection of the entire house, as shown in Figure 13.2.
Consider a computer-aided design (CAD) program that stores an internal representation of your 3-D house plans and can compute any 2-D view that you ask. It may seem that this contradicts the rule that “projections cannot add information that does not already exist,” because not every possible view already exists in the 3-D internal representation. But it is OK for the CAD program to transform its internal representation to show a view, which may require it to calculate and display a cross-section. What the rule prohibits is views that would be impossible to derive from the 3-D internal representation, such as a new room, or a garage.
Although you will use a lot of graphical views, some of the most useful are views textual or tabular. Figure 13.3 shows a view of the house that lists the costs. You could draw it graphically, but it would be easier and better to use a spreadsheet program.
Figure 13.2: A two dimensional (2-D) floorplan view (i.e., a projection) of a three dimensional (3-D) house model.
This section is extracted from the book.



